平面向量基本定理是学好、用好平面向量的精髓所在，很多向量或几何问题，若不注重平面基本定理的应用，是会走很多弯路的。

今天要说的等和线定理，其实就是平面向量基本定理的一个重要推论——“共线定理”，但它的作用却是不可小觑的，一旦用好它，便能直捣黄龙，一举破题！

课本上有多处出现了“等和线”的基本题型，其理论基础多次被提及。

此类题目要求学生在数形结合，转化化归等数学思想上有很高的理解，对于此类题目学生普遍束手无策。

学生在解决此类问题时，往往要通过建系或者利用角度与数量积处理，思路不清晰且解题繁琐，得分率普遍不高。故做此专题，希望能给出一个简单的方法解决此类问题。

齐头并进 -平面向量之等和线定理

01 招式赏析

以2017年全国III卷选择压轴题第12题为例，我们知道，该题利用建系法结合直线与圆的位置关系也可以求解，但计算量偏大，且考查知识比较综合，考生在考场上必然要花费不少时间，且还容易出错。

而如果能会利用等和线定理来求解，会显得简单很多，当然前提条件是理解透彻该定理，故设计本解题招式——齐头并进，相信通过对该招式的剖析，定会让你体验到等和线定理的妙不可言。

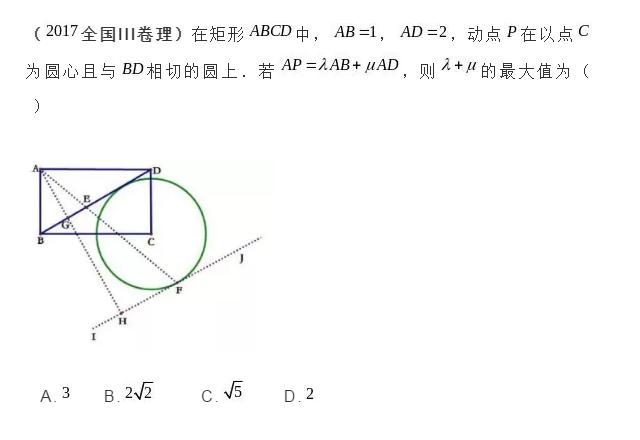
02 见招拆招

通过对高考真题的赏析，结合平面向量共线定理，引申出等和线定理问题模型，让你清楚等和线定理其实就是平面向量共线定理的推论，做到知其然知其所以然。

向量问题等和线的运用

1.适用题型

平面向量基本定理的表达式中，研究两系数的和差及线性表达式的范围与最值。

2.基本定理

03 招式套路

当然，只知其所以然还不行，还要清楚等和线定理的具体用处，所以给出等和线的具体类型，解题思想，解题套路，方能知己知彼。

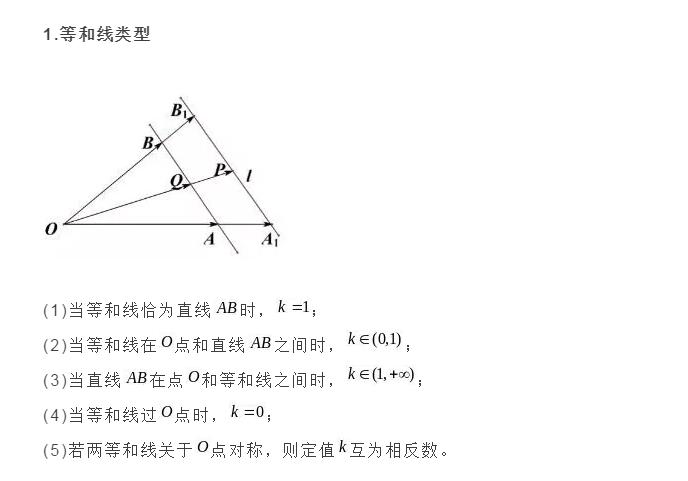
2.解题步骤

1.确定等和线为1的线；

2.平移(旋转或伸缩)该线，结合动点的可行域，分析何处取得最大值和最小值；

3.从长度比或者点的位置两个角度，计算最大值和最小值。

说明：平面向量共线定理的表达式中的三个向量的起点务必一致，若不一致，本着少数服从多数的原则，优先平移固定的向量；若需要研究的两系数的线性关系，则需要通过变换基底向量，使得需要研究的代数式为基底的系数和。

04 招式实战

要知道，知己知彼，一战方休，实战才能见真章！同学们要通过类似题型的练习，体会等和线定理解决问题的效果，掌握一个解题大招，解决一类典型问题，快速提分，轻松应考！

（以下提供一些类似的题型，同学们可以一展身手，将此招式学以致用，举一反三！需要解析的同学们可以在后台回复“齐头并进”，即可获取题目解析哦！）

平面向量在高考中为必考高频考点，有单独考查，亦经常渗透到其它考点，多以平面图形为主，涉及动点、最值问题已经是考查的主流趋势，多数同学解决此类问题，方法是以建系为主，基底为辅，简单题建系耗时间，难题目建系运算量大！

等和线定理的应用其实可以辅助我们秒解这类最值问题，若要熟练应用，需不断实践，慢慢沉淀！

除“齐头并进”外，还有很多关于数学解题的招式，如：运用“庖丁解牛”解决范围问题；运用“借花献佛”解决放缩法证明不等式问题；运用“颠倒乾坤”解决等体积法求距离问题……趣味招式，招招制胜！

如果你对这些招式感兴趣，千万不能错过即将上线的《高考抢分五十招》，这绝对是你数学高考复习的一大秘籍！